排序简析

快速排序

选择一个目标值，比它小的放左边，比它大的放右边，目标值的位置已经确定，再分别对左边和右边进行快排

不稳定 O(nlogn)

    function quickSort(array) {
      if (array.length < 2) {
        return array;
      }
      const target = array[0];
      const left = [];
      const right = [];
      for (let i = 1; i < array.length; i++) {
        if (array[i] < target) {
          left.push(array[i]);
        } else {
          right.push(array[i]);
        }
      }
      return quickSort(left).concat([target], quickSort(right));
    }

归并算法

分而治之：将数组递归成完全二叉树，每个节点使用合并算法。

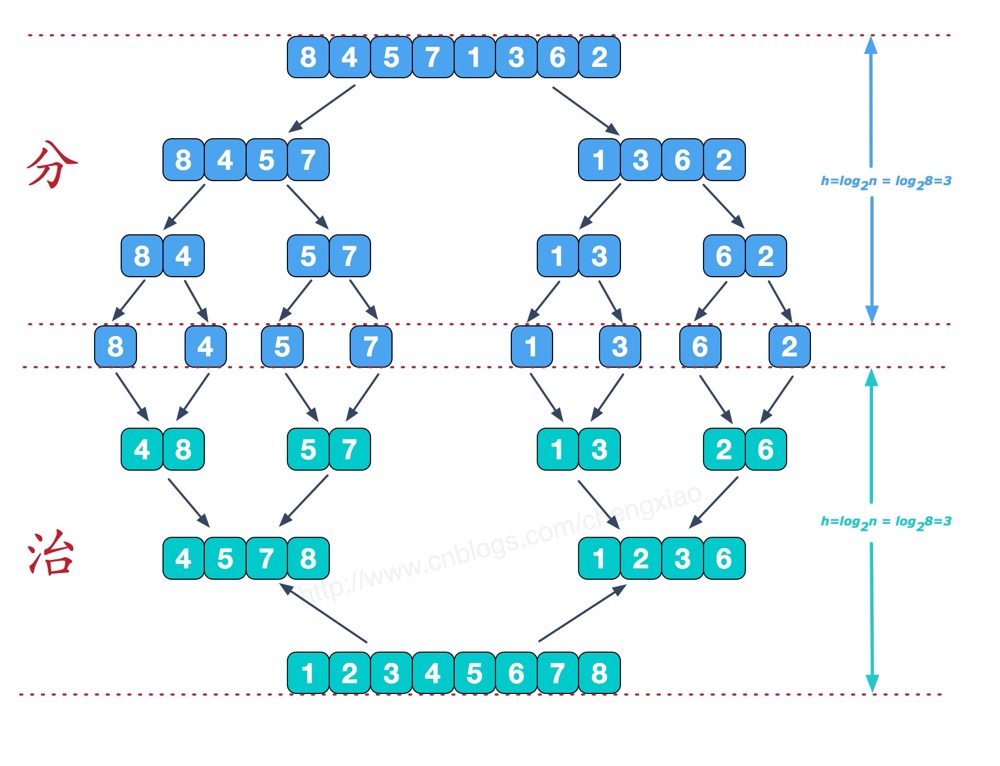
稳定 O(nlogn)

//二分为完全二叉树
function mergeSort(arr){
	if(arr.length<2) return arr;
  let mid = Math.floor(arr.length/2);
  let left = arr.slice(0,mid);
  let right = arr.slice(mid);
  return merge(mergeSort(left),mergeSort(right))
}
//合并法则，merge的时候，说明left,right内部已经有序
function merge(left,right){
	let tmp = [];
  while(left.length&&right.length){
  	if(left[0]<right[0]){
    	tmp.push(left.shift());
    }else{
    	tmp.push(right.shift());
    }
  }
  while(left.length){
  	tmp.push(left.shift());
  }
  while(right.length){
  	tmp.push(right.shift());
  }
  return tmp;
}

选择排序

每次排序，将最小的或者最大的值放在前面的有序数列中

把后面数组中最小值按顺序往前面放。

步骤：

因为每一次循环，都可能会交换位置，所以也可以理解为交换排序。

循环遍历每一项，将该项和她后面的数中最小值作比较，如果大于最小值，则互换位置。

不稳定 O(n^2)

不稳定，O(n^2)

function chooseSort(arr){
	for(let i = 0;i<arr.length-1;i++){
    let minIndex = i;
  	for(let j = i+1;j<arr.length;j++){
    	if(arr[j]<arr[minIndex]){
      	minIndex = j;
      }
    }
    [arr[minIndex],arr[i]] = [arr[i],arr[minIndex]];
  }
}

插入排序

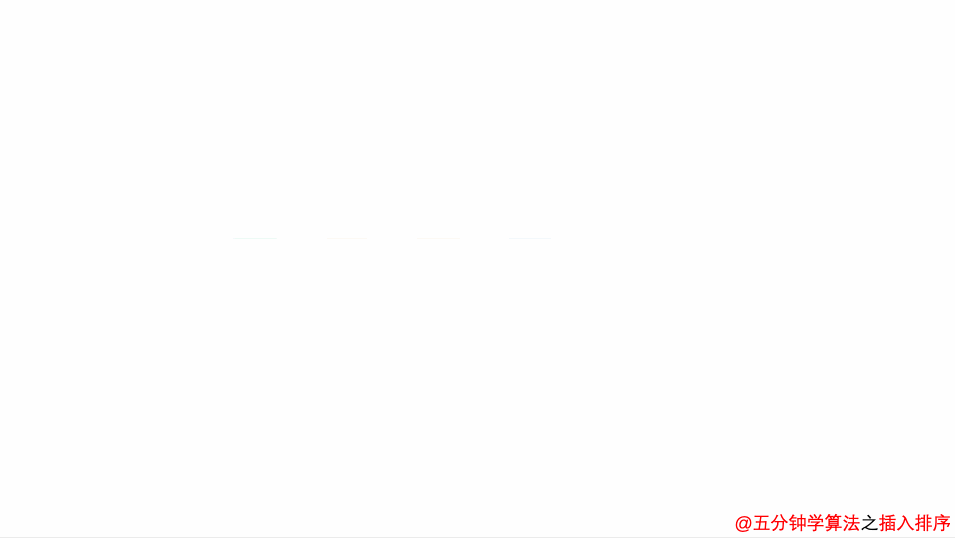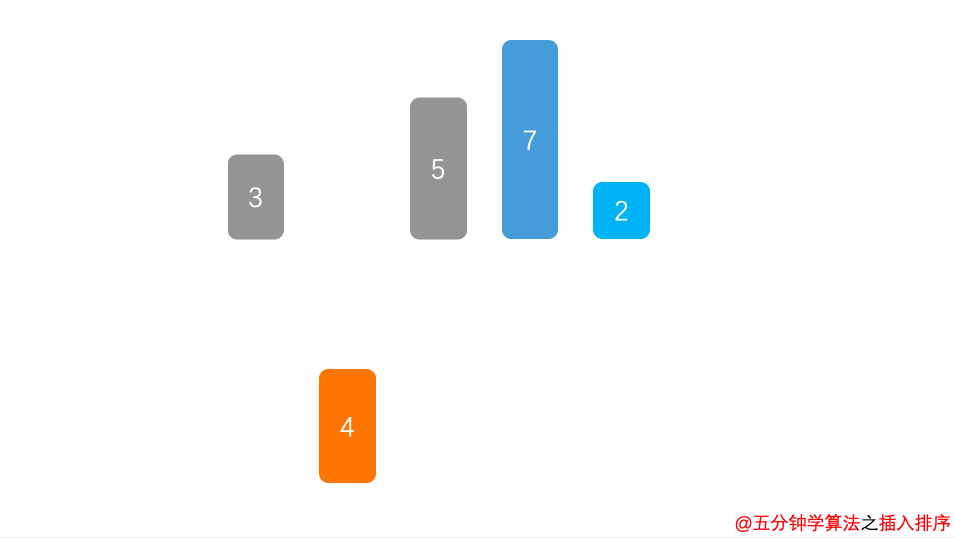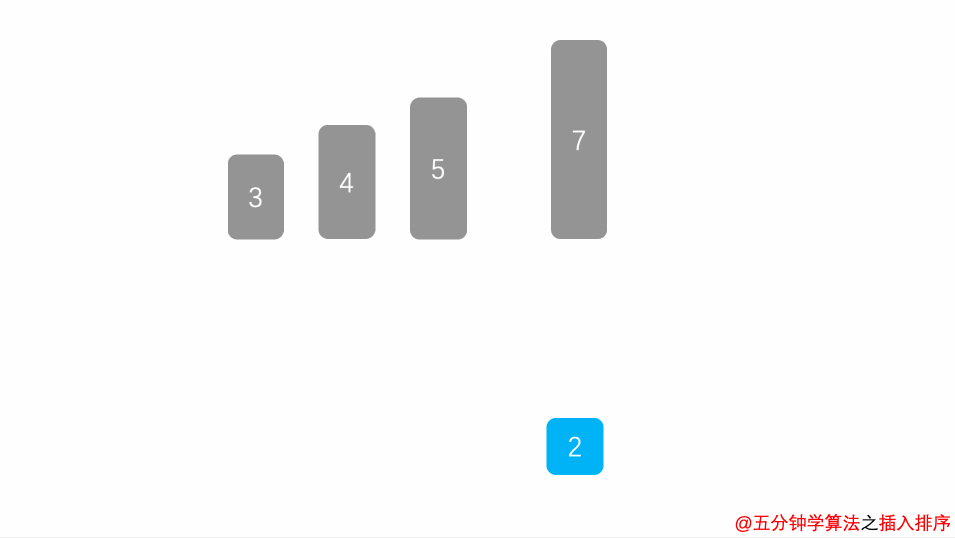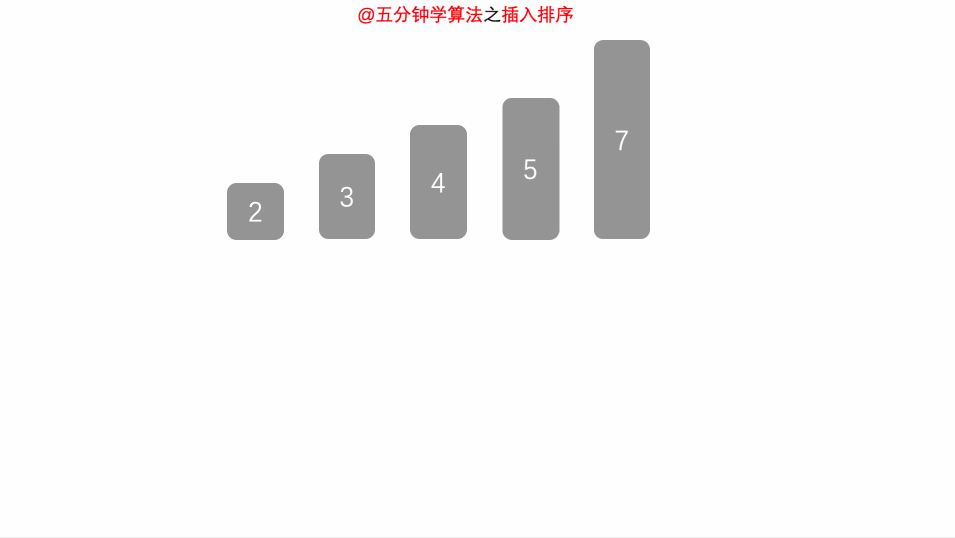
将左侧序列看成一个有序序列，每次将一个数字插入该有序序列。插入时，从有序序列最右侧开始比较，若比较的数较大，后移一位；较小则跳出循环。

在前面的有序数组中找到自己位置。

步骤：

1. 从第二项开始循环，跟它前面的项进行比较（直到找到第一个比它小的值，然后插入到其后面）
2. 从后往前比较，大的就交换位置
3. 小的就结束循环

稳定 O(n^2)

function insertSort(arr) {
    for (let i = 1; i < arr.length; i++) {
        let target = i;
        for (let j = i - 1; j >= 0; j--) {
            if (arr[target] < arr[j]) {
                [arr[target], arr[j]] = [arr[j], arr[target]];
                target = j;
            } else {
                break;
            }
        }
    }
    return arr;
}

冒泡排序

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

优化：当一次循环没有发生冒泡，说明已经排序完成，停止循环。

稳定 O(n^2)

function BubbleSort(arr) {
    //外层循环是控制次数，需要length-1次
    for (let i = 0; i < arr.length - 1; i++) {
        //每次循环用一个标签优化，如标签没变说明已经排好序
        let flag = true;
        //里层循环，相邻比较，还得删除已经拍好序的项，边界法
        for (let j = 0; j < arr.length-1 - i; j++) {
            if (arr[j] > arr[j+1]) {
                flag = false;
                [arr[j], arr[j+1]] = [arr[j+1], arr[j]];
            }
        }
        if(flag){
            break;
        }
    }
    return arr;
}

堆排序

1. 创建一个大顶堆，大顶堆的堆顶一定是最大的元素。
2. 交换第一个元素和最后一个元素，让剩余的元素继续调整为大顶堆。
3. 从后往前依次和第一个元素交换并重新构建，排序完成。

不稳定 O(nlogn)

function heapSort(array) {
    let arr = array.slice(0);
    createMaxHeap(arr);//此时已经是最大堆了，第一个数是最大值
    //从后往前遍历，每次将最大值和最后一位交换，剩下无序项继续最大堆化
    for (let i = arr.length - 1; i > 0; i--) {
        [arr[0], arr[i]] = [arr[i], arr[0]];
        max_heapify(arr, 0, i);
    }
    return arr;
}
function createMaxHeap(arr) {
    let len = arr.length;
    //数组的前半段都是父节点，从后往前遍历
    for (let i = Math.floor(len / 2) - 1; i >= 0; i--) {
        max_heapify(arr, i, len);
    }
}
function max_heapify(arr, start, end) {
    let dad = start;
    let son = dad * 2 + 1;
    //左子节点超出数组范围，退出，这里的end是数组长度
    if (son >= end) {
        return;
    }
    //如果右节点存在，且右节点>左节点,son加一，最后用大一点的子节点和父节点交换
    if (son + 1 < end && arr[son + 1] > arr[son]) {
        son++;
    }
    //父节点和大一点的子节点交换
    if (arr[dad] <= arr[son]) {
        [arr[dad], arr[son]] = [arr[son], arr[dad]];
        max_heapify(arr, son, end);//子节点继续最大堆化
    }
}